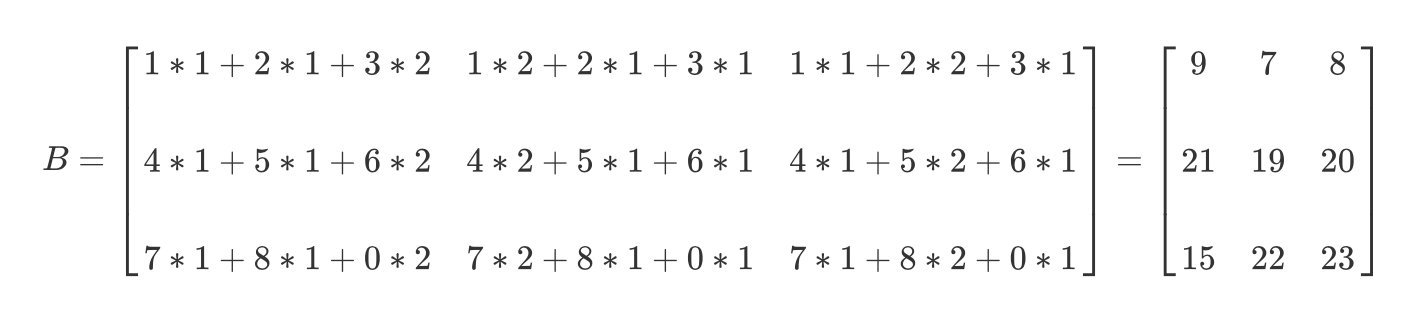1. 4.6 数学：矩阵

1.1. 学习目标

• 知道什么是矩阵和向量
• 知道矩阵的加法,乘法
• 知道矩阵的逆和转置
• 应用np.matmul、np.dot实现矩阵运算

1.2. 1 矩阵和向量

1.2.1. 1.1 矩阵

矩阵，英文matrix，和array的区别矩阵必须是2维的，但是array可以是多维的。

如图:这个是 3×2 矩阵，即 3 行 2 列，如 m 为行，n 为列，那么 m×n 即 3×2 $\left[ \begin{matrix} 1 & 2 \\\\ 3 & 4 \\\\ 5 & 6 \end{matrix} \right]$ 矩阵的维数即行数×列数

矩阵元素(矩阵项): $A = \left[ \begin{matrix} 1 & 2 \\\\ 3 & 4 \\\\ 5 & 6 \end{matrix} \right]$ Aij 指第 i 行，第 j 列的元素。

1.2.2. 1.2 向量

向量是一种特殊的矩阵，讲义中的向量一般都是列向量，下面展示的就是三维列 向量(3×1)。 $A = \left[ \begin{matrix} 1 \\\\ 2 \\\\ 3 \end{matrix} \right]$

1.3. 2 加法和标量乘法

矩阵的加法:行列数相等的可以加。

例: $\left[ \begin{matrix} 1 & 2 \\\\ 3 & 4 \\\\ 5 & 6 \end{matrix} \right] + \left[ \begin{matrix} 1 & 2 \\\\ 3 & 4 \\\\ 5 & 6 \end{matrix} \right] = \left[ \begin{matrix} 2 & 4 \\\\ 6 & 8 \\\\ 10 & 12 \end{matrix} \right]$ 矩阵的乘法:每个元素都要乘。

例: $3 * \left[ \begin{matrix} 1 & 2 \\\\ 3 & 4 \\\\ 5 & 6 \end{matrix} \right] = \left[ \begin{matrix} 3 & 6 \\\\ 9 & 12 \\\\ 15 & 18 \end{matrix} \right]$ 组合算法也类似。

1.4. 3 矩阵乘法

1.4.1. 3.1 矩阵向量乘法

矩阵和向量的乘法如图：m×n 的矩阵乘以 n×1 的向量，得到的是 m×1 的向量

例: $\left[ \begin{matrix} 1 & 3 \\\\ 4 & 0 \\\\ 2 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 \\\\ 5 \end{matrix} \right] = \left[ \begin{matrix} 16 \\\\ 4 \\\\ 7 \end{matrix} \right]$

1*1+3*5 = 16
4*1+0*5 = 4
2*1+1*5 = 7

矩阵乘法遵循准则：

(M行, N列)*(N行, L列) = (M行, L列)

1.4.2. 3.2 矩阵和矩阵乘法

矩阵乘法：

m×n 矩阵乘以 n×o 矩阵，变成 m×o 矩阵。

举例：比如说现在有两个矩阵 A 和 B，那 么它们的乘积就可以表示为图中所示的形式。

练一练 $A= \left[ \begin{matrix} 1 & 2 & 3 \\\\ 4 & 5 & 6 \\\\ 7 & 8 & 0 \end{matrix} \right] B= \left[ \begin{matrix} 1 & 2 & 1 \\\\ 1 & 1 & 2 \\\\ 2 & 1 & 1 \end{matrix} \right]$ 求矩阵AB的结果

答案：

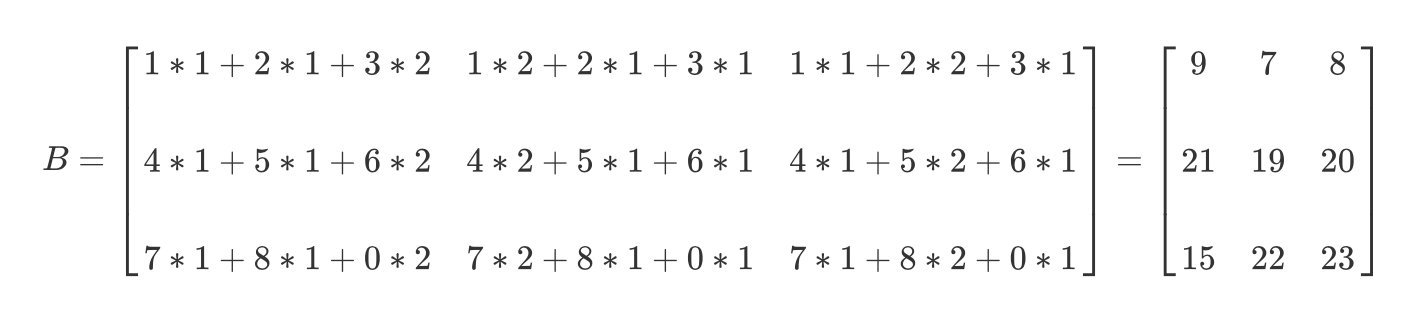
1.4.3. 3.3 矩阵乘法的性质

矩阵的乘法不满足交换律：A×B≠B×A

矩阵的乘法满足结合律。即：A×（B×C）=（A×B）×C

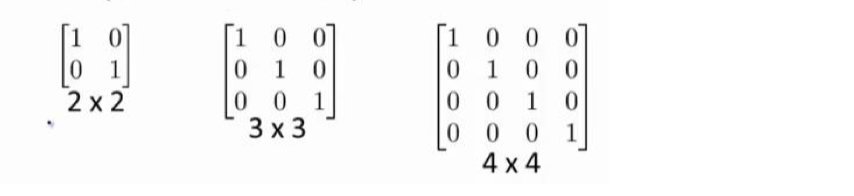
单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的 1,我们称 这种矩阵为单位矩阵．它是个方阵，一般用 I 或者 E 表示，从 左上角到右下角的对角线（称为主对角线）上的元素均为 1 以外全都为 0。如：

1.5. 4 逆、转置

矩阵的逆：如矩阵 A 是一个 m×m 矩阵（方阵），如果有逆矩阵，则：

AA-1 = A-1A = I

低阶矩阵求逆的方法:

• 1.待定系数法
• 2.初等变换
• ……

矩阵的转置：

• 设 A 为 m×n 阶矩阵（即 m 行 n 列），第 i 行 j 列的元素是 a(i,j)，即：A=a(i,j)

• 定义 A 的转置为这样一个 n×m 阶矩阵 B，满足 B=a(j,i)，即 b (i,j)=a (j,i)（B 的第 i 行第 j 列元素是 A 的第 j 行第 i 列元素），记 AT =B。

• 直观来看，将 A 的所有元素绕着一条从第 1 行第 1 列元素出发的右下方 45 度的射线作 镜面反转，即得到 A 的转置。

例： $\left[ \begin{matrix} a & b \\\\ c & d \\\\ e & f \end{matrix} \right]^T = \left[ \begin{matrix} a & c & e \\\\ b & d & f \end{matrix} \right]$

1.6. 5 矩阵运算

$\left[ \begin{matrix} 80 & 86 \\\\ 82 & 80 \\\\ 85 & 78 \\\\ 90 & 90 \\\\ 86 & 82 \\\\ 82 & 90 \\\\ 78 & 80 \\\\ 92 & 94 \end{matrix} \right]* \left[ \begin{matrix} 0.3 \\\\ 0.7 \end{matrix} \right]= \left[ \begin{matrix} 84.2 \\\\ 80.6 \\\\ 80.1 \\\\ 90 \\\\ 83.2 \\\\ 87.6 \\\\ 79.4 \\\\ 93.4 \end{matrix} \right]$

1.6.1. 5.1 矩阵乘法api介绍

• np.matmul
• np.dot

>>> a = np.array([[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]])
>>> b = np.array([[0.7], [0.3]])

>>> np.matmul(a, b)
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])

>>> np.dot(a,b)
array([[81.8],
       [81.4],
       [82.9],
       [90. ],
       [84.8],
       [84.4],
       [78.6],
       [92.6]])

np.matmul和np.dot的区别:

二者都是矩阵乘法。

• np.matmul中禁止矩阵与标量的乘法。
• 在矢量乘矢量的內积运算中，np.matmul与np.dot没有区别。

1.7. 6 小结

• 1.矩阵和向量【知道】
  • 矩阵就是特殊的二维数组
  • 向量就是一行或者一列的数据
• 2.矩阵加法和标量乘法【知道】
  • 矩阵的加法:行列数相等的可以加。
  • 矩阵的乘法:每个元素都要乘。
• 3.矩阵和矩阵(向量)相乘 【知道】
  • (M行, N列)*(N行, L列) = (M行, L列)
• 4.矩阵性质【知道】
  • 矩阵不满足交换率,满足结合律
• 5.单位矩阵【知道】
  • 对角线都是1的矩阵,其他位置都为0
• 6.矩阵运算【掌握】
  • np.matmul
  • np.dot
  • 注意：二者都是矩阵乘法。 np.matmul中禁止矩阵与标量的乘法。 在矢量乘矢量的內积运算中，np.matmul与np.dot没有区别。